MTL Annual Research Report 2013

Building Compressed Sensing Systems

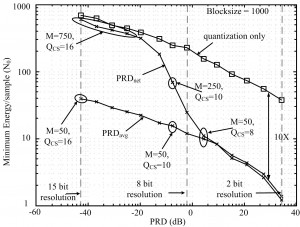
Compressed sensing (CS) is a sub-Nyquist sampling technique^[1] with under-explored implementation potential. In this multi-disciplinary project, we analyze CS circuit architectures from a hardware implementation perspective^[2],^[3], develop and apply end-to-end evaluation methodologies from a system perspective^[4],^[5], and support experiments by analyses from a theoretical perspective^[6]. We have considered the practical aspects of CS applied to both wireless sensors and Analog Information Converters (AICs).  For the former, we showed that a digital CS-based sensor system is efficient and robust. By data compression alone, CS enables over 10X energy reduction in transmission energy; see Figure 1. CS is robust to channel errors, and amenable to simple schemes to enable 4X energy reduction^[4]. For the latter (AICs), we evaluated the ability of CS to overcome resolution/performance limitations of Nyquist-rate high-speed sampling (limited by jitter, aperture and other circuit impairments). We find AICs have no performance advantage over high-speed ADCs. In standard architectures, signal encoding is realized with a mixer-like circuit, which still operates at Nyquist frequency to avoid input aliasing. Our evaluation shows that AICs are resolution limited, though they may enable a 2x energy reduction for low amplifier gains and very sparse signals^[5].

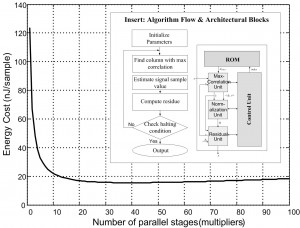
There is little literature on CS recovery hardware. As an initial step, we explored the implementation design space for a matching pursuit (MP) algorithm; see Figure 2 (insert)^[7]. We chose MP as it is the simplest possible recovery algorithm, so that we may gain critical first insights. MP is a greedy (iterative) algorithm that estimates a sparse sample in each iteration and produces the full estimate once it halts. The figure also shows the basic implementation blocks where we found that the max-correlation unit, which consists of multipliers, dominates the energy expenditure. The energy-cost evaluation in Figure 2 shows diminishing returns around 20 multipliers, at 1 V supply, in 45-nm CMOS technology.  Overall, at 8 bits resolution and 10 fixed iterations, the energy cost of recovery is 2.8 nJ/sample, with an area of 0.4 mm² at a minimum-energy throughput of 2.5 mega-samples/s at 0.4 V supply. Since the algorithm is block-parallel, a further throughput increase comes with a linear increase in area.

1. E. Candes and T. Tao, ”Decoding by Linear Prog.,” IEEE Transactions on Information Theory, vol. 51, no. 12, pp. 4203-4215, Dec. 2005. [↩]
2. F. Chen, A. P. Chandrakasan, and V. Stojanovic, ”Design and Analysis of a Hardware-Efficient Compressed Sensing Architecture for Data Compression in Wireless Sensors” IEEE Journal of Solid-State Circuits, vol. 47, no. 3, pp. 744-756, Mar. 2012. [↩]
3. F. Chen, A. Chandrakasan, V. Stojanovic, and E. Alon, “A Signal-agnostic Compressed Sensing Acquisition System for Wireless and Implantable Sensors,” in Proc. IEEE Custom Integrated Circuits Conference, Sep. 2010. [↩]
4. F. Chen, F. Lim, O. Abari, A. Chandrakasan, and V. Stojanovic, “Energy-Aware Design of Compressed Sensing Sys, for Wireless Sensors under Performance and Reliability Constraints,” IEEE Transactions on Circuits and Systems I, vol. 60, no. 3, pp. 650-661, Mar. 2013. [↩] [↩]
5. O. Salehi-Abari, F. Chen, F. Lim, and V. Stojanovic, “Performance Trade-offs and Design Limitations of Analog-to-Information Converter Front-Ends,” in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, Mar. 2012. [↩] [↩]
6. F. Lim and V. Stojanovic, ”U-statistics and Compressed Sensing I: Non-Asymptotic Average-Case Analysis,” IEEE Transactions on Signal Processing, vol. 61, no. 10, pp. 2473-2485, May 2013. [↩]
7. O. Salehi-Abari, “Building Compressed Sensing Systems:  Sensors and Analog-to-Information Converters,” Master’s thesis, Massachusetts Institute of Technology, Cambridge, 2012. [↩]