Uncertainty Quantification for the Periodic Steady State of Forced and Autonomous Circuits
- Category: Circuits & Systems
- Tags: luca daniel, zheng zhang
Designers are particularly interested in periodic steady-state (PSS) analysis when designing analog/RF circuits or power electronic systems. Such circuits include both forced (e.g., amplifiers, mixers, power converters) and autonomous cases (also called unforced circuits, e.g., oscillators). Popular PSS simulation algorithms include shooting Newton, finite difference, harmonic balance, and their variants. As devices scale down to the nanometer scale, almost all performance metrics are influenced by manufacturing process variations. This work focuses on the uncertainty quantification (UQ) of PSS solutions influenced by process variations.
Specifically, this work proposes a simulator for the UQ of PSS solutions based on the stochastic testing (ST) method[1]. After expressing the node voltages and branch currents as a truncated generalized polynomial chaos (gPC) expansion, we apply the shooting Newton method to solve for the PSS gPC coefficients. For forced circuits, the shooting Newton method is directly applied to the resulting ST formulation. For unforced circuits, since the oscillation period depends on statistical device parameters, a scaling scheme is applied to the time axis before applying shooting Newton. For both forced and autonomous circuits, decoupled solvers are developed to accelerate the numerical computation.
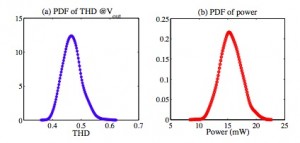
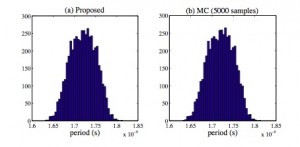
Our algorithms have been tested by several analog/RF circuits with both Gaussian and non-Gaussian random parameters. Figure 1 shows the calculated density function of the total harmonic distortion (THD) and power dissipation of a CMOS low-noise amplifier (LNA) under threshold voltage variation and linear device mismatch. Using our decoupled solver leads to 13 times of speedup. Figure 2 shows the histograms of the frequency of a BJT Colpitts oscillator, simulated by our proposed PSS UQ tool and standard Monte Carlo with 5000 samples. Both methods produce the same statistical distribution for the signal gain, but our ST method is about 700 times faster. Both methods achieve the same level of accuracy (with 1% error), but our proposed UQ tool is about 428 times faster than the conventional Monte Carlo simulator.
- Figure 1: Density function of the total harmonic distortion (THD) and power consumption of a low-noise amplifier (LNA) from our proposed solver.
- Figure 2: Histograms of the oscillation frequency of a Colpitts oscillator, obtained by our proposed simulator (left) and standard Monte Carlo simulation (right).
- Z. Zhang, T. A. El-Moselhy, I. Elfadel and L. Daniel, “Stochastic testing method for transistor-level uncertainty quantification based on generalized polynomial chaos,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, to be published. [↩]