MTL Annual Research Report 2013

Stochastic Testing Method for Transistor-level Uncertainty Quantification

Design and fabrication uncertainties have become an important issue in nano-scale integrated circuit design. Such uncertainties are typically randomly distributed, as described by probability density functions extracted from measurements. Such device-level uncertainties can propagate to the upper circuit level, leading to significant variations in circuit performances (such as power dissipation, small-signal gain, clock frequency, etc.) As a result, many performance metrics become uncertain in today’s IC design. Therefore, it is highly desirable to develop efficient electronic design automation (EDA) tools to capture the variations in various design levels.

This work develops a non-Monte Carlo stochastic circuit simulator for uncertainty quantification of nonlinear circuits. This simulator is based on generalized polynomial chaos (gPC) and a newly developed stochastic testing scheme. The gPC allows our platform to simulate integrated circuits with both Gaussian and non-Gaussian random parameters. Meanwhile, the stochastic testing method allows using fast decoupled numerical solvers with adaptive time stepping, leading to superior efficiency over existing stochastic Galerkin and stochastic collocation methods. Different types of simulations (such as DC, AC, transient, periodic steady-state) are implemented, and they are tested on several analog, RF, digital circuit netlists, as well as power electronic circuits, including both forced and autonomous circuits. Significant speedup is observed compared with Monte-Carlo simulation, as well as existing intrusive and non-intrusive spectral methods.

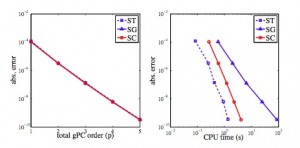
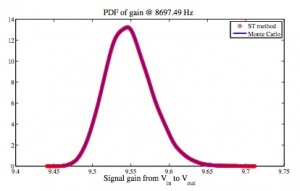
Figure 1 compares the numerical errors of our ST method with stochastic Galerkin (SG) and stochastic collocation (SC), using a CMOS low-noise amplifier (LNA) as an example. Clearly, the proposed ST solver has an accuracy similar to that of SG and SC methods. However, ST is more efficient over the existing spectral methods. Figure 2 shows the AC analysis results using our ST method versus standard Monte Carlo simulation. Both methods produce the same statistical distribution for the signal gain, but our proposed ST method is about 700 times faster.