Self-similarity of Contact Line Depinning from Textured Superhydrophobic Surfaces

  • Authors: A. T. Paxson, K. K. Varanasi
  • Sponsorship: Department of Mechanical Engineering, Massachusetts Institute of Technology
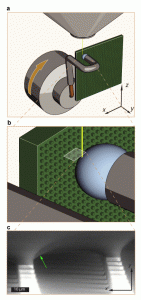
Figure 1: ESEM fixture and micrograph. (a) Experimental apparatus within an ESEM chamber. A water droplet is held against a vertically oriented superhydrophobic micropillar surface by a copper wire. Water drop is cooled by a Peltier device and can be swept across the surface (x-direction) by rotating the ESEM stage about the y-axis. (b) Illustration of electron beam imaging area with respect to droplet contact line. (c) Single micrograph from video of water droplet receding along superhydrophobic micropillars in positive x-direction.

Figure 1: ESEM fixture and micrograph. (a) Experimental apparatus within an ESEM chamber. A water droplet is held against a vertically oriented superhydrophobic micropillar surface by a copper wire. Water drop is cooled by a Peltier device and can be swept across the surface (x-direction) by rotating the ESEM stage about the y-axis. (b) Illustration of electron beam imaging area with respect to droplet contact line. (c) Single micrograph from video of water droplet receding along superhydrophobic micropillars in positive x-direction.

We report a technique for observing the dynamic behavior of a liquid contact line on superhydrophobic surfaces at high magnification using environmental scanning electron microscopy (ESEM). Superhydrophobic surfaces utilize a combination of low surface energy and high roughness that lead to a Cassie-Baxter (CB) wetting state, in which the drop sits atop roughness features on a composite interface[1][2][3]. Adhesion is substantially reduced in the CB state, but it is not altogether eliminated. In fact, the adhesion of CB drops represents an almost ideal case of strong dilute defects for investigating the effects of contact line pinning[4]. When a CB drop is moved across a surface, the deformations due to pinning are localized at the receding region; as the contact line is displaced, it is hypothesized that micro-capillary bridges are formed at each pinning site[5][6][7]. The behavior of these capillary bridges ultimately determine the adhesion of the entire drop. In the current study, we are able to capture micron-scale images of capillary bridges formed as the contact line recedes across a superhydrophobic micropillar surface (Fig. 1) and measure the local receding contact angle. We find that it is equivalent to the macroscale receding contact angle observed on a chemically equivalent smooth surface and satisfies the Gibbs depinning criterion[8]. On a dual-hierarchy surface consisting of roughened micropillars, the capillary bridges exhibit a larger local receding angle. We attribute these effects to a self-similar depinning mechanism that depends on the pinned fraction of the contact line at each roughness hierarchy. We develop a model to predict adhesion force of a macroscopic drop and verify this mechanism with adhesion measurements. This mechanism helps to explain the necessity for multiple length scales exhibited by lotus leaves and other superhydrophobic surfaces and also helps explain how complicated pillar geometries lead to increased pinning.

  1. A. Lafuma and D. Quéré, “Superhydrophobic states,” Nat. Mater., vol. 2, no. 7, pp. 457–460, 2003. [↩]
  2. L. Bocquet and E. Lauga, “A smooth future?,” Nat. Mater., vol. 10, no. 5, pp. 334–337, 2011. [↩]
  3. H. Y. Erbil et al., “Transformation of a simple plastic into a superhydrophobic surface,” Science, vol. 299, no. 5611, pp. 1377–1380, 2003. [↩]
  4. M. Reyssat and D. Quéré, “Contact Angle Hysteresis Generated by Strong Dilute Defects†,” J. Phys. Chem. B, vol. 113, no. 12, pp. 3906–3909, 2009. [↩]
  5. J. F. Joanny and P. G. de Gennes, “A model for contact angle hysteresis,” J. Chem. Phys., vol. 81, no. 1, pp. 552–562, Jul. 1984. [↩]
  6. D. Öner and T. McCarthy, “Ultrahydrophobic surfaces. Effects of topography length scales on wettability,” Langmuir, vol. 16, no. 20, pp. 7777–7782, 2000. [↩]
  7. S. Herminghaus, “Roughness-induced non-wetting,” Eur. Lett., vol. 52, pp. 165–170, 2000. [↩]
  8. J. W. Gibbs and H. A. Bumstead, Scientific Papers of J. Willard Gibbs …: Thermodynamics. Longmans, Green and Company, 1906. [↩]

Faculty & Topics