Partial Differential Equation-Integral Equation (PDE-IE) Solvers for Electromagnetic Scattering
Domain decomposition concepts, combined with other high performance scientific computation technologies, provide a framework to hybridize different solvers together and thus allow engineers to explore a greater complexity of physics in multi-domain electromagnetic scattering models. Multi-solver domain decomposition method (MS-DDM) significantly enhances the solution of hybrid, multi-domain electromagnetic, scattering, and radiation problems involving electrically large and complex structures. The computational domain is decomposed into sub-regions based on the local material properties and geometrical characteristics. Each sub-region is solved by employing the best suitable computational electromagnetic technique. The coupling between sub-regions is carried out through the Robin-type transmission conditions (Robin TC), enforcing both electric and magnetic field continuities and improving the convergence of the overall iterative solution.
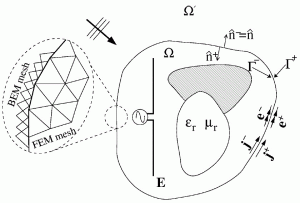
In this project, a PDE-IE solver is integrated to simulate multi-scale electromagnetic scattering problems (Figure 1). Both finite element method (FEM) and boundary element method (BEM) domains are modularly treated in terms of meshing, selection of basis functions, matrix assembling, and even the solution process[1][2][3]. When the concept of domain decomposition is employed, the FEM sub-region is decomposed into a boundary integral (BI) domain and an FEM domain, which are connected through the use of Robin TC, as shown in Figure 2. Robin TC mimics an impedance boundary condition, which causes smaller reflection at the boundary for the propagating mode and guarantees the convergence for the propagation mode. Double layer cement variables defined on the interior and exterior sides of the artificial surface enclosing the FEM sub-region allow different mesh or basis functions on FEM and BEM sides (nonconforming mesh).
The generated global matrix is symmetric and free of internal resonances. Several techniques, including the discrete empirical interpolation method (DEIM), are being explored to obtain a low rank representation of the dense blocks in the global system matrix[4]. In addition, fast algorithms, such as pre-corrected FFT (pFFT), are being studied, in conjunction with the techniques above, to significantly reduce the computational cost and memory requirement[5] for solving BEM regions.
- Figure 1: FEM-BEM domain decomposition and cement variables.
- Figure 2: Robin transmission conditions.
- K. Zhao, V. Rawat, and J.-F. Lee, “A domain decomposition method for electromagnetic radiation and scattering analysis of multi-target problems,” IEEE Trans on Antennas and Propagation, vol. 56, no. 8, pp. 2211-2221, 2008. [↩]
- M. Vouvakis, K. Zhao, S.-M. Seo, J.-F. Lee, “A domain decomposition approach for non-conformal couplings between finite and boundary elements for unbounded electromagnetic problems in R3,” Journal of Computational Physics, vol. 225, no. 1, pp. 975–994, 2007. [↩]
- X. Wang, Z. Peng, K.-H. Lim, and J.-F. Lee, “Multisolver domain decomposition method for modeling EMC effects of multiple antennas on a large air platform,” IEEE Trans on Electromagnetic Compatibility, vol. 54, no. 2, pp. 375-388, 2012. [↩]
- M. Barrault, Y. Maday, N. C. Nguyen, and A. T. Patera, “An empirical interpolation method: Application to efficient reduced-basis discretization of partial differential equations,” Comptes Rendus Mathematique, vol. 339, no. 9, pp. 667-672, 2004. [↩]
- J. R. Phillips and J. K. White, “A precorrected-FFT method for electrostatic analysis of complicated 3D structures,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, pp.1059-1072, 1997. [↩]