Numerical Computation Platform Designed for Optimization
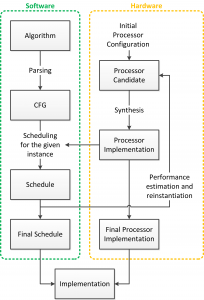
Significant effort is spent researching hardware and software acceleration of basic building blocks for numerical computation[1][2][3]; however, the majority of the previous work focuses on either hardware or software independently. In this work we develop hardware and software together, as shown in Figure 1, providing tight design-time coupling between them, with the ultimate goal of exploring numerical hardware platform tradeoffs at both limits of performance: high speed and low power.
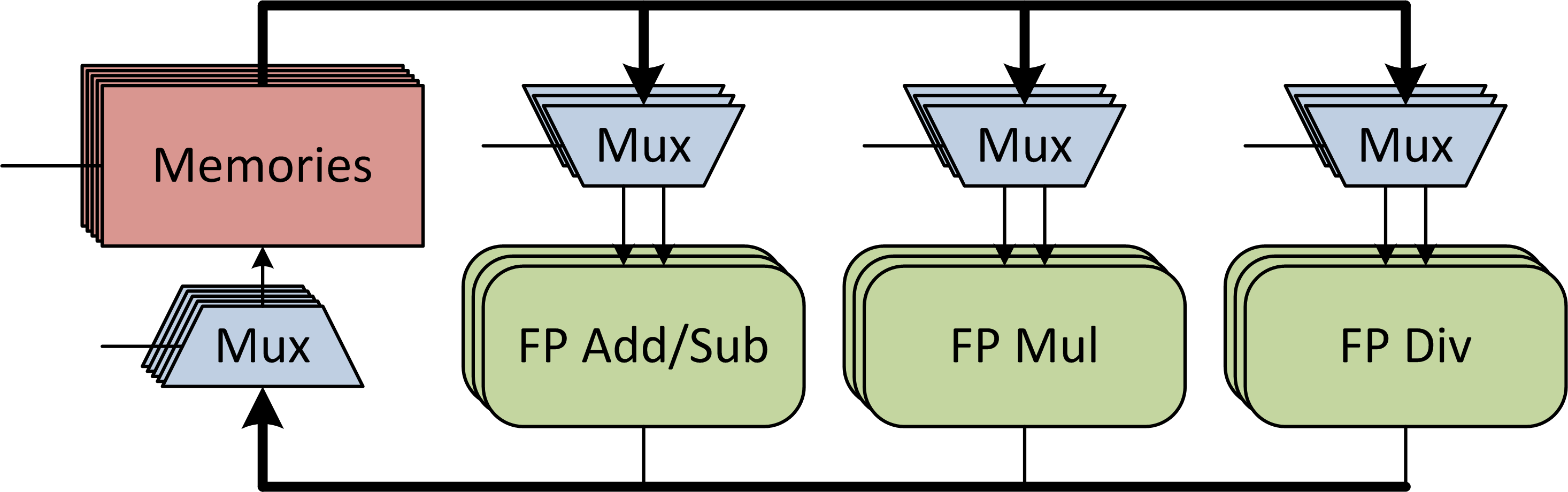
For tight coupling of the algorithm and processor physical layer constraints, our project is centered on the link between these layers: an optimizing compiler. Algorithm optimization begins with synthesizing the computation graph from the written algorithm. Next the graph is optimized through constant folding, dead-code elimination and similar compiler techniques. Additionally tree-rebalancing optimizations are performed to allow for serial associative operations to occur in parallel. Extensive scheduling sweeps are then performed for various processor microarchitectures to find the optimal software/hardware pair. The specifications are fed to an abstract processor template to generate a custom processor similar to the one shown in Figure 2 to run the optimal software. This processor template is written in Bluespec to allow us to postpone decisions on a number of details such as the number and types of processing units, the number and size of memories, the pipeline depths of the floating-point units, and the interconnect structure.
The generated processors are currently synthesized onto a prototyping FPGA platform to confirm our compiler predictions. We see a strong run-time dependence on processor microarchitecture for a given algorithm. Reductions up to 4x in overall latency can be obtained by proper processor configuration, validating a meta-programming approach to processor logic-level design. Furthermore, we show that the optimal latency point is neither at the minimum cycle count nor at the highest clock frequency, but somewhere in between that depends on the topology of the computational flow graph.
- Figure 1: The design process for optimized hardware and software for computation applications.
- Figure 2: Architecture of a custom numerical computation processor generated by the processor template.
- J. Mattingley and S. Boyd, “Real-Time Convex Optimization in Signal Processing,” IEEE Signal Processing Magazine, vol. 27, no. 3, pp. 50-61. [↩]
- K. V. Ling, S. P Yue,. and J. M. Maciejowski, “A FPGA implementation of model predictive control,” 2006 American Control Conference, pp. 1930-1935. [↩]
- B. Leung, et al., 2010. “An Interior Point Optimization Solver for Real Time Inter-Frame Collision Detection: Exploring Resource-Accuracy-Platform Tradeoffs,” 2010 International Conference on Field Programmable Logic and Applications, pp.113-118. [↩]