MTL Annual Report

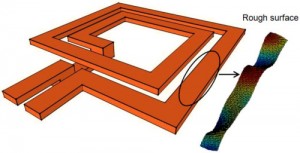
Figure 1: Geometry of a two-turn, 1-mm side-length, square inductor with surface roughness. The inductor is discretized using 2.500 spatial elements. The roughness is modeled using 400 random parameters.

Uncertainties in the integrated circuit manufacturing processes typically result in interconnect structures, whose dimensions and shapes deviate from the original design intent. Such geometrical variations are typically assumed to be random, and they affect the electrical performance of the manufactured interconnect structures. Consequently, the effect of such variations on the electrical performance of the manufactured interconnects needs to be estimated and accounted for during the design phase. To achieve such an objective, one needs to develop efficient variation-aware parasitic extraction tools. There are two different categories of algorithms for variation-aware extraction, namely, “intrusive” and “non-intrusive.” “Non-intrusive” algorithms are those that rely on sampling the parameter space and then using any standard deterministic solver to compute a deterministic solution at the different sampling points. The main challenge facing such methods is the need to simultaneously and efficiently solve a very large number of linear systems corresponding to each different sample point. The term “intrusive” refers to the fact that the solution is computed using specialized stochastic algorithms, such as the stochastic Galerkin method ^[1], the Neumann expansion ^[2], or the Combined Neumann-Hermite Expansion ^[3].

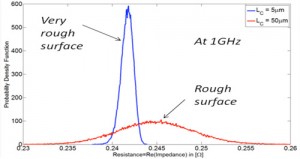
Figure 2: Probability density function of the input resistance for two different roughness profiles.

In this project we present a novel intrusive stochastic algorithm ^[4]. The main idea behind our algorithm is to search simultaneously in both the spatial and stochastic spaces for dominant basis vectors whichbest represent the unknown solution. We formulate a simple nonlinear optimization problem which uncovers sequentially the most dominant basis vectors in the combined spatial-stochastic space. The main computational advantage of the proposed approach stems from the fact that at every step of the algorithm, only two dominant basis vectors, one in the spatial space and another in the stochastic space, are simultaneously computed. The two dominant bases are computed such that the equation residual is minimized. After each step both the solution and the equation residuals are updated. The algorithm is terminated when the norm of the equation residual is sufficiently small. Consequently, the algorithm provides meaningful error measures that determine the quality of the solution. The final complexity of our algorithm scales with the sum (rather than the product) of the sizes of the spatial and stochastic spaces. Hence, it is orders of magnitude more efficient than many of the available state-of-the-art techniques. Finally, we validate our algorithm on a variety of on-chip and off-chip capacitance and inductance extraction problems, of moderate size. In addition we solve a variety of very large size problems, which cannot be solved using any of the available state-of-the-art techniques.

1. R. Ghanem and P. Spanos, Stochastic Finite Elements: A Spectral Approach. Spring-Verlag, 1991. [↩]
2. Z. Zhu and J. White, “FastSies: A Fast Stochastic Integral Equation Solver for Modeling the Rough Surface Effect,” IEEE/ACM International Conference on Computer Aided Design, Nov. 2005, pp. 675-682. [↩]
3. T. Moselhy and L. Daniel, “Stochastic Integral Equation Solver for Variation-Aware Interconnect Extraction,” Design Automation Conference, June 2008. [↩]
4. T. Moselhy and L. Daniel, “Stochastic Dominant Singular Vectors Method for Variation-Aware Extraction,” to be presented at Design Automation Conference, June 2010. [↩]