MTL Annual Report

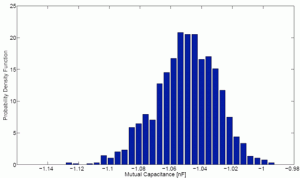
Figure 1: A parallel plate capacitor with an upper rough surface, discretized using more than 20,000 spatial elements. Stochastic variation is modeled using 323 independent random variables.

Uncertainties in the integrated-circuit manufacturing processes typically result in interconnect structures whose dimensions and shapes deviate from the original design intent. Such geometrical variations are typically assumed to be random and to affect the electrical performance of the manufactured interconnect structures. Consequently, the effects of such variations on the electrical performance of the manufactured interconnects need to be estimated and accounted for during the design phase. To achieve such an objective, one needs to develop efficient variation-aware parasitic extraction tools. There are two different categories of algorithms for variation-aware extraction, namely, “intrusive” and “non-intrusive.” In “intrusive” solvers the unknown is computed using specialized stochastic solvers such as the stochastic Galerkin method ^[1], the Neumann expansion ^[2] or the combined Neumann-Hermite expansion ^[3]. On the other hand, “non-intrusive” algorithms, such as the Monte Carlo Method, are those that rely on sampling the parameter space and then using any standard deterministic solver to compute a deterministic solution at the different sampling points.

Figure 2: Probability density function of the mutual capacitance of the parallel plate conductor.

“Non-intrusive” sampling based methods are embarrassingly parallel and can easily exploit the state-of-the-art “fast” solvers. Consequently, such methods are of great practical importance. However, one of the remaining computational challenges of sampling-based methods is how to simultaneously and efficiently solve the large number of linear systems corresponding to each different sample point. In this project we present a new non-intrusive algorithm based on a stochastic model reduction technique ^[4]. The main idea is to exploit the similarity among the different linear systems of equations in order  to reduce the computational complexity of solving the entire set of linear systems of equations. We first propose a projection matrix which guarantees  that the statistical moments (and/or the coefficients of the projection of the stochastic vector on some orthogonal polynomials) are preserved when computed using the reduced model. We further introduce a proximity measure, which is used to cheaply determine if the available reduced basis accurately represents the solution at a new point in the parameter space, or if instead the reduced basis needs to be expanded. Finally, in order to reduce the time required for the system assembly, we use the multivariate Hermite expansion to represent the system matrix. We verify our method by solving a variety of variation-aware capacitance extraction problems ranging from on-chip capacitance extraction in the presence of width and thickness variations, to off-chip capacitance extraction in the presence of surface roughness. We further solve very-large-scale problems that cannot be handled by any other state-of-the-art technique.

1. R. Ghanem and P. Spanos, Stochastic Finite Elements: A Spectral Approach. Spring-Verlag, 1991. [↩]
2. Z. Zhu and J. White, “FastSies: A Fast Stochastic Integral Equation Solver for Modeling the Rough Surface Effect,” IEEE/ACM International Conference on Computer Aided Design, Nov. 2005, pp. 675-682. [↩]
3. T. Moselhy and L. Daniel, “Stochastic Integral Equation Solver for Variation-Aware Interconnect Extraction,” Design Automation Conference, June 2008. [↩]
4. T. Moselhy and L. Daniel, “Variation-Aware Interconnect Extraction using Statistical Moment Preserving Model Order Reduction,” in Design Automation and Test in Europe, March 2010. [↩]