MTL Annual Report

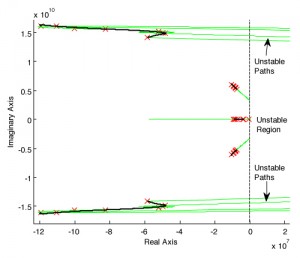
Figure 1: Plot showing the trajectory of poles with parameter variation. Thick black lines trace the poles’ location from our stable parameterized model, while thin grey (or green) lines trace the poles’ location from the unconstrained fit (which clearly becomes unstable as indicated by the arrows).

System-level design optimization has recently started drawing the attention of circuit designers. A system-level optimizer would search over the entire design space, defined by the parameters of interest. Such optimizers therefore require the availability of parameterized compact dynamical models of individual modules. The parameters may include geometrical quantifiers, such as width and spacing for an on-chip inductor, or design parameters such as center frequency or characteristic impedance in the case of distributed transmission line structures. The parameterized models of individual blocks need to be compact and stable since the optimizer would be solving ordinary differential equations (using time-domain integration or periodic steady-state methods) to compute the performance metrics.

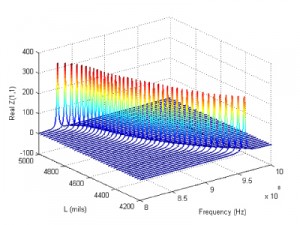
Figure 2: Surface traced by the real part of the frequency response of the parameterized model of patch antenna over parameter sweep.

In this project we have developed a method for generating parameterized models of linear systems that the user will be able to instantiate for any parameter value. Given a collection of systems swept over design and geometrical parameters of interest, we identify a closed-form parameterized dynamical model using constrained fitting. The proposed algorithm is completely independent from the type of initial non-parameterized identification procedure used for the individual systems. In other words, the individual (non-parameterized) models may be generated by any stability-preserving modeling scheme, such as convex optimization based approaches ^[1] [2] or vector-fitting-based approaches ^[3] [4]. The models are first converted into an equivalent pole-residue form. Final parameterized models are developed by polynomial or rational multivariate approximation between residue matrices, system poles and direct matrix. We have finally showed the effectiveness of the proposed approach by modeling several practical circuit blocks. Figure 1 plots the trajectory of poles in response to parameter variation. Figure 2 plots the real part of frequency response of our stable parameterized model as a function of densely sampled parameter values.

1. Z. Mahmood, B. Bond, T. Moselhy, A. Megretski, L. Daniel, “Passive reduced order modeling of multiport interconnects via semidefinite programming,” In the Proc. of Design Automation &Test in Europe (DATE) Conference, March 2010. [↩]
2. K. C. Sou, A. Megretski, and L. Daniel, “A quasi-convex optimization approach to parameterized model order reduction,” IEEE Trans. On Computer-Aided Design of Integrated Circuits and Systems, 27(3), March 2008. [↩]
3. S. Grivet-Talocia and A. Ubolli, “A comparative study of passivity enforcement schemes for linear lumped macromodels,” IEEE Trans. On Advanced Packaging, 31(4), Nov. 2008. [↩]
4. B. Gustavsen and A. Semlyen, “Rational approximation of frequency domain responses by vector fitting,” IEEE Trans. on Power Delivery, 14(3), July 1999. [↩]