MTL Annual Report

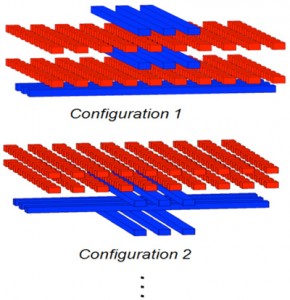
Figure 1: Five layer configurations. Each layer has a different dielectric constant. Different configurations are constructed by different orderings of the five layers. Each configuration is composed of 209 conductors.

With the adoption of restricted design rules (RDR) and ultra-regular fabric paradigms for controlling design printability at the 22nm node and beyond, there is an emerging need for a layout-driven, pattern-based parasitic extraction of alternative fabric layouts. Such paradigms impose two requirements of micro- and macro-regularity on the layouts. “Micro-” regularity is achieved by restricting shape edges to lie on a restricted design grid that also imposes stringent directionality on shape orientation. “Macro-” regularity is achieved by using a very restricted set of litho-friendly logic cells. Such regularities have motivated using a relatively small number of optimized (litho-friendly and robust) layouts as building blocks to construct any arbitrary structure. These building blocks will be referred to subsequently as “motifs.” A designer typically examines different arrangements of the “motifs” in order to choose the “optimal” (in terms of printability, area, and electrical performance) design. Consequently, from an extraction point of view, there is a need to develop tools that are aware of topological variations.

Figure 2: Markov Transition Probability associated with one of the layers.

In this project, we propose a hierarchical floating random walk (HFRW) ^[1] [2] algorithm for computing the 3D capacitances of a large number of topologically different layout configurations that are all composed of the same layout motifs. Our algorithm is not a standard hierarchical domain decomposition extension of the well established floating-random-walk technique ^[3] [4] but rather a novel algorithm that employs Markov Transition Matrices (MTMs). Specifically, we first compute for each motif an MTM, representing the probability of making a transition from any point on the motif boundary to any point on the motif boundary or on a surface of the conductors inside the motifs. Then the capacitance of the different layout configurations is extracted by using the pre-computed motif MTM to form a large Markov Chain, and finally by simulating such a chain using random walks. The complexity of our algorithm is primarily related to the computation of the motif MTM. Such computation needs to be performed once for each motif, independent of the number of configurations. On the other hand, the complexity of simulating the Markov Chains (computing the configuration) is almost negligible. Consequently, the main practical advantage of the proposed algorithm is its ability to compute the capacitance of a set of layout configurations in a complexity that is basically independent of the set size. For instance, in a large 3D layout example, the capacitance calculation of 120 different configurations made of similar motifs is accomplished in the time required to solve independently just 2 configurations, i.e., a 60× speedup.

1. T. El-Moselhy, I. M. Elfadel and L. Daniel, “A hierarchical floating random walk algorithm for fabric-aware 3D capacitance extraction,” Proceedings of the 2009 IEEE/ACM International Conference on Computer Aided Design, November 2009. [↩]
2. T. El-Moselhy, I. M. Elfadel, and L. Daniel, “A Markov Chain Based Hierarchical Algorithm for Fabric-Aware Capacitance Extraction,” accepted for publication in Transaction on Advanced Packaging. [↩]
3. R. B. Iverson and Y. L. Le Coz, “A Stochastic Algorithm for High Speed capacitance Extraction in Integrated Circuits,” Solid-State Electronics, Vol. 35, No. 7, pp. 1005–1012, 1992. [↩]
4. T. El-Moselhy, I. M. Elfadel , and L. Daniel, “A capacitance solver for incremental variation-aware extraction,” Proceedings of the 2008 IEEE/ACM International Conference on Computer-Aided Design, November 2008 [↩]